前缀和:求某个区间或区域的和
差分:为某个连续区间或区域加一个固定的值
「一维前缀和」
- Analyse
求一段区间的和
-
code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15# input, 0位置存储0,从1开始存数 n,m=map(int, input().split()) a=[0] a.extend(list(map(int, input().split()))) b=[0]*(n+1) # 前缀和 for i in range(1,n+1): b[i] = b[i-1]+a[i] # output while m: m-=1 l,r=map(int, input().split()) print(b[r]-b[l-1])
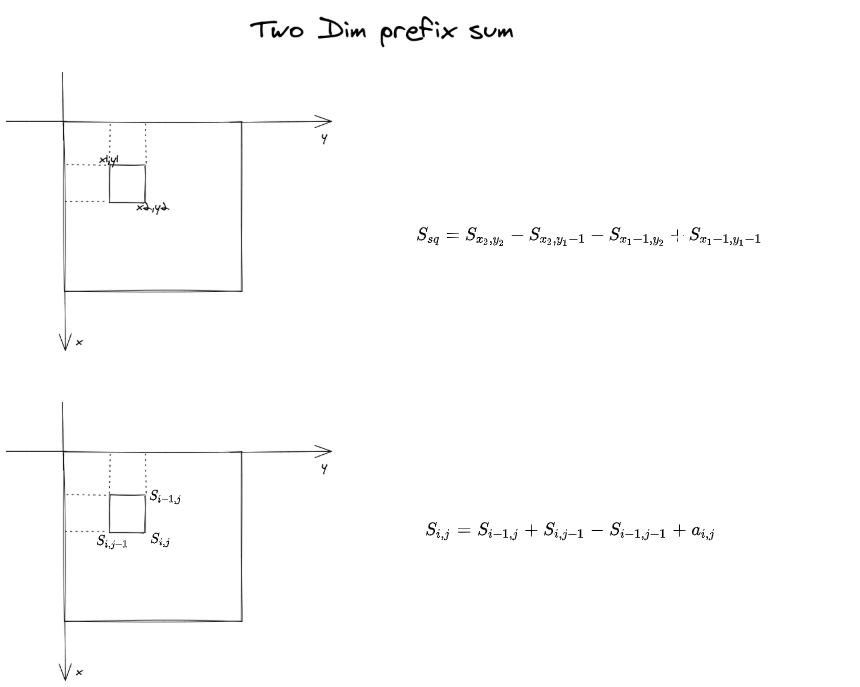
「二维前缀和」
- Analyse
-
code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20# input n,m,q=map(int,input().split()) a=[[0 for i in range(m+1)] for j in range(n+1)] b=[[0 for i in range(m+1)] for j in range(n+1)] for i in range(1,n+1): temp=list(map(int, input().split())) for j in range(m): a[i][j+1] = temp[j] # 前缀和 for i in range(1,n+1): for j in range(1,m+1): b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j] # output while q: q-=1 x1,y1,x2,y2=map(int, input().split()) print(b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1])
「一维差分」
- Analyse
- 想让区间的数,如果让,会使的前缀和数组位置后面的所有数都会, 所以问题来了,怎么能使位置后面的数不加呢? 即可。

- code
|
|
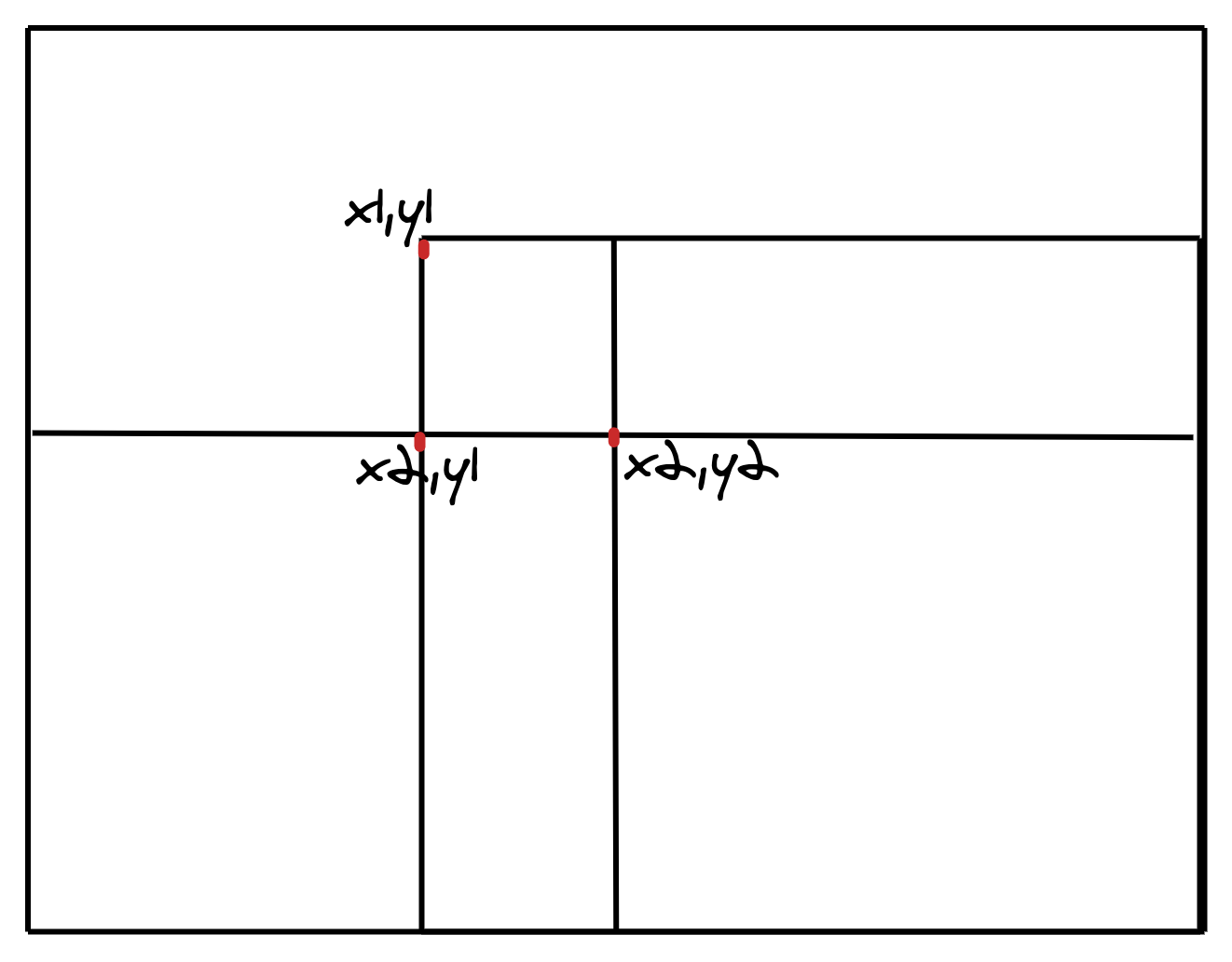
「二维差分」
- Analyse
- 同一维差分原理一致,从给某个区间变成给某个矩形区域加 c,只需推导公式即可.
- Code
|
|